How do I get an intuitive
understanding of the origin of the acoustic peaks?
How do I get an intuitive
understanding of the origin of the acoustic peaks?
Submitted anonymously by a senior colleague!
(These peaks in the "power spectrum" of CMB anisotropies are caused by the effect of large-scale sound waves around the time the photons were last scattered.)
I think that's a good question! The answer lies in the fact that the whole heuristic explanation is a bit confused about whether it's in real space or Fourier space. Plus it avoids any mention of gauge choice (ie exactly what you do above the horizon size) etc. So to some extent the basic picture doesn't stand up too well to such questioning! All that aside, I think it is possible to answer your question simply. You should think of this overdense blob as getting a kick from gravity when it comes inside the horizon (ie becomes causal) - thus it is a driven acoustic oscillation. So you would expect the "starting point" to be the equilibrium then the radiation falls into the potential well, ie it goes to maximum compression, then bounces back (due to the baryon pressure) to overshoot the equilibrium and become a rarefaction. I hope this helps!
I have been reading tons of
technical papers and the idea of an "angular power spectrum" keeps popping
up. It's hard to bridge the gap in this field between the extremely
low-level information and the extremely technical. What is this entity?
Прислал jlh22"AT"dana.ucc.nau.edu
Different experiments are sensitive to different angular scales. Think of a CMB experiment as measuring a set of temperature of the sky in "pixels" of some angular size (set by the smallest scale which can be resolved by the particular telescope) over some region of the sky. The size of the pixel and the size of the region of sky are the smallest and largest angular scale that are probed. The information obtained from a CMB experiment is then the variation in the temperatures at some particular angular scale, or perhaps a range of different angular scales.
For the COBE satellite, for example, these variations in temperature were measured over a range of angular scales from about 7o up to the full sky. Other experiments tend to have higher angular resolution and also cover just a small fraction of the sky. When we put together a whole bunch of measurements at different angular scales we end up with an estimate of how the temperature variations change as we change the angular scale. A plot of this, ie "temperature variation" versus angular scale, is referred to as an "angular power spectrum" -- it's the amount of "power" in the temperature fluctuations plotted as a function of angle.
In fact you want to be more mathematically precise than this, and instead of "angular scale", you really want to deal with the amplitudes of a set of functions which are independent of each other and which probe different angular scales. Such functions for the sphere are called "spherical harmonics", and have well-understood properties. The spherical harmonic which describes variation over the whole sky is called the "monopole", while variations of 180o are described by the "dipole", variations on scales of 90o are described by the "quadrupole" and so on. The index of the harmonic is the "multipole" number, so that a small multipole number corresponds to large angle, and a large multipole number corresponds to a small angle. What is actually plotted then is the square of the amplitudes of these spherical harmonics versus the multipole number. This is the "angular power spectrum", and it can be interpretted as meaning the variation in temperatures as a function of angular scale (size of "pixel"), plotted so that large angles are on the left and small angles on the right.
I am having difficulty understanding how the odd acoustic peaks in the
power spectrum can correspond to fluctuation compressions, while the even
peaks correspond to rarefactions. It seems to me that
we should see equal power in compression and rarefaction.
Прислал desai"AT"orca.astro.washington.edu 2/99
Ah, a technical question! The details of how the microwave background fluctuations vary with angular scale can be somewhat esoteric - however, the basics are pretty straightforward: the density perturbations were oscillating, and we catch them "frozen" at the last scattering epoch. The big bump in the spectrum corresponds to the scale that was first feeling the causal effects of gravity at that time, while smaller scales had already been oscillating for a while. Both compressions and rarefactions lead to enhancements in the temperature fluctuations at those particular angular scales, and so the "power spectrum of anisotropies" ends up as a series of bumps and wiggles.
The specific question (posed by desai) concerns the peaks that come from the compressions versus those that come from the rarefactions. The reason they're not exactly equal is that there's an effect from the regular matter (baryons) which essentially shifts the zero point. This is fairly well explained in the excellent summary called "The Physics of Microwave Background Anisotropies", by Hu, Sugiyama & Silk, which appeared in Nature in 1997, and can be found as a postscript file here. If this seems too complex, you might like to start with the article by Scott & White, called "Echoes of Gravity", which is here.
Why is the background microwave radiation found to be so smooth
since surely a lumpy distribution is necessary to explain the
very uneven distribution of matter in the universe?
Прислал degs"AT"iafrica.com 10/99
This is a good question, and one which many people were asking prior to the detection of the CMB anisotropies in 1992. Up until then there had only been upper limits to the lumpiness of the CMB sky. The point was that it was difficult to construct models in which the COBE satellite would see complete smoothness, and that would be consistent with the idea that the structure we observe in today's Universe grew through the steady action of gravity. Many people suggested that if COBE gave further upper limits, then we would need to consider much more complicated ideas for how structure formed.
In fact the amount of variation observed in the microwave sky is almost exactly what was predicted based on the most popular models (where the Universe is dominated by some form of so-called Cold Dark Matter). So the CMB sky is just as lumpy as it should be (about 1 part in 100,000) to lead to all the lumpiness we see today, with the simple attractive force of gravity being all that is required to increase that lumpiness over the last 10 or so billion years.
Do the tiny CMB anisotropies constrain the mean mass density of the
Universe in any way, and if it does, why?
Прислал ib6146"AT"bristol.ac.uk 11/99
The anisotropies in the CMB can be measured as a function of angular scale. Schematically, what you do is make a map of the CMB sky with a certain resolution of pixels, and estimate the variance of the temperature in that map - then smooth the map to a bigger pixel size and repeat. You end up with a bunch of numbers that tell you how "lumpy" the microwave sky is at various angular sizes (technically what is measured is called the "power spectrum", which is really just a better defined version of this same procedure).
It turns out that theories for the formation and evolution of structure in the Universe give quite detailed predictions for this "power spectrum". In particular, the simplest models (compatible with a theory called "inflation", which generated the fluctuations in the very early Universe) predict stronger anisotropies around a scale of about 1 degree on the sky. This seems to be pretty much what the most recent expermental results have been showing.
In a little more detail, the robust prediction of the models is for a characteristic length scale on the sky (corresponding roughly to the distance light can have travelled in the age of the Universe at the time when the CMB last scattered off matter). This length scale will look like a different angular scale on the sky depending on the "curvature" of the Universe. Since the curvature is governed by the mass-energy density content of the Universe, then the precise angular scale of maximum CMB variations on the sky depends on the density of the Universe.
The best available data suggest that these simple theories seem to be a good fit, and that the Universe must be rather close to being "flat" (ie not very curved at all). Since the matter that we can account for comprises only about one third of what is required to make the Universe flat, then there seems to be evidence from the CMB for some additional form of energy that helps keep the Universe flat. This is variously called the "cosmological constant", "qunitessence" or "dark energy". But just because it has several names, it doesn't mean we really understand what it is!
Could you give me the angle formed between the rotation axis of Earth
and the axis of the anisotropy dipole of CMB.
Прислал mcrotti"AT"inlab.com.ar
As you no doubt know (if you've read any of the rest of this page at least!), there is a so-called "dipole" pattern on the CMB sky. In other words one half of the sky is a little hotter than average and one side a little colder. This is a Doppler effect, casused by our motion through the Universe.
Precisely what direction you give for this dipole depends on what other velocities you have subtracted off first. For example, we know that the Sun is moving around our Galaxy, so do you want the dipole in the rest frame of the Sun or the rest frame of the Galaxy? For the Solar System, the answer is that the motion is towards celestial coordinates RA (longitude) = 11.20 hours (or 168o), Dec (latitude) = -7.2o. Since this coordinate system has the "celestial equator" defined as the projection of the Earth's equator on the sky, then our motion is -7.2o from the equator. So the answer to your question is that the Solar System is moving through the Cosmos at an angle of approximately 83o from the Earth's South Pole.
In fact the annual variation in the Dipole, casued by the Earth's motion around the Sun, can also be seen by an all-sky experiment that lasts more than a year. This is a direct measurement of the Earth's motion, and in a sense proves that the Earth is going round the Sun rather than the Sun going round the Earth (not that this has been doubted for a few hundred years!). The COBE satellite detected this annual variation so well that it could be used to calibrate the instrument - since we know precisely how fast the Earth is going round the Sun (30 km/s), then we know precisely how big a variation should be measured.
What are the standard model CMBR anisotropies and how do they come about?
Прислал mbliss"AT"oberon.ark.com 2/00
The CMB anisotropies come about from a combination of effects due to interaction of photons with perturbations in the density of the Universe on a range of scales. Various aspects of this question are discussed in answer to other questions on this page.
There is really no "standard model" as such. The general paradigm that seems to fit best is that the initial perturbations were of the sort produced during an inflationary period in the very early Universe (which isn't necessairly to say that inflation happened!). These evolved from being initially of roughly the same amplitude at each scale, to the situation we observe today where they vary with scale in a complex way. This variation encodes the values of a number of fundamental parameters which describe our Universe: the average density in each of the important components, including each form of dark matter; the expansion rate; the amplitude and scale-dependence of the initial density perturbations; the contribution from gravity waves; and some recent processing of the anisotropies by scattering in the reionized Universe, gravitational lensing and other effects.
The promise of the new CMB experiments is that we will ultimately know the values of these parameters. Assuming that this "standard paradigm" (inflationsry-insipred cold dark matter dominated Universes) continues to look good, then the experiments will nail down the parameters and provide us with a detailed "standard model". The alternative is that the general picture fails to fit everything, implying either that there is some crucial missing ingredient, or some whole new paradigm is required. The new CMB experiments should tell us that also.
After comparing several sources, I have noticed that there are different
numbers where isotropy is concerned...is it 1/1000, 1/10,000, or 1/100,000?
Прислал JULIE108"AT"aol.com 4/00
It depends exactly what you mean by isotropy.
The CMB sky is totally smooth down to one part in 1000. At that level you notice that one side of the sky is hotter than the other side of the sky. This is the "dipole" caused by our motion through the Universe. So you can say that the sky is isotropic to 1 part in 1000.
When you subtract off this motion effect you find the remaining temperature map of the sky is incredibly smooth. You don't see any features in this map until you get down to the 1 part in 100,000 level. The sky has an overall temperature near 3 Kelvin, while these anisotropies are differences in temperature which are typically tens of micro-Kelvins. So apart from the motion effect, the CMB sky is isotropic at the level of about 1 part in 100,000.
Assumption #1: There are no preferred inertial frames, leads to general
relativity... but the CMB provides a preferred inertial frame. If the CMB
obeys the laws of physics, and it shows the way to a preferred inertial frame,
then physics as a whole is not the same in all frames, in contradiction to
Assumption #1.
Прислал smithe"AT"mrcwdc.com 4/00
Although I've answered similar questions before, I know that this concept is still troubling to some people. So let me make a couple of additional remarks here. Firstly, the description of an expanding Universe involves general relativity, and not special relativity. So it's not necessarily the case that you should expect the ideas of special relativity (which are, let's face it, less general!) to apply. Special relativity doesn't really deal with non-inertial frames. So, for example, you can in principle (described consistently within general relativity) discover observationally that the Universe is rotating, even although (within the context of special relativity) your inclination might be to ask "rotating with respect to what?".
But more importantly you have to examine the assumptions more closely. Let us go back to Einstein. A translation of his original 1905 statement is: The same laws of electrodynamics and optics are valid for all frames of reference for which the equations of mechanics hold good. We will raise this conjecture (the purport of which will hereafter be called the `Principle of Relativity') to the status of a postulate...
There is indeed a frame of reference (actually it's expanding, but never mind that!) in which the CMB dipole would be measured to be zero. But there is nothing special about the laws of physics in that frame. Photons behave as you expect, the laws of electromagnetism are no different, and F=ma is still true.
I dont understand why the variance of energy distribution isnt
calculated which depends on the square of planck's spectral fn and Bose
statistics. Is this due to plasma formation prior to photon gas
formation?
I'm afraid I don't understand this question.
The CMB is composed of photons, which follow the so-called Planck function (the blackbofy shape to the spectrum), and are governed by the so-called Bose statistics (since photons are bosons). However, the fluctuations in photon number caused by those Bose statistics have no cosmologically observable effects that I can think of.
How are the parameters calculated and verified from the observations?
Прислал ian.watson0"AT"tinyonline.co.uk 6/00
This is another great question. However, I'm afraid that a full answer would be very long, and also rather technical! This in fact is what I spend a bunch of my time doing research on, so I could very easily bore you here!
The short answer is that the fundamental observable is the CMB anisotropy "power spectrum", which tells you how the variations in temperature depend on angular scale. This power spectrum can be calculated for simple models of the origin and evolution of the fluctuations - which grow into our present-day structure and leave their imprint on the CMB sky. These predictions give a power spectrum which contains a series of what are often referred to as "bumps and wiggles"! The details of these features depend on the precise values of the cosmological parameters which describe our Universe (densities in each of the species of matter, expansion rate, a couple of parameters to describe the initial state of the fluctuations, some recent astrophysical processing effects, etc.).
When you have a decent CMB anisotropy data-set you can try to fit the power spectrum estimate, and then constrain the various parameters to the ranges where the models fit the data. At the moment the flatness of the Universe (essentially the sum of all the densities in components of matter and energy) is well constrained, and there are some limits on other parameters too. But we're still in the situation where the answer depends to a large extent on how wide a range of models you're prepared to consider. Things will continue to get better as the bumps and wiggles are pinned down more accurately. It is realistic to expect that in the near future the CMB (in combination with other cosmological measurements) will allow quite precise determination of most of the important parameters simultaneously.
There have been many relevant articles at a range of levels, in various magazines and journals. In the UK, you could check out back issues of New Scientist for example. If you can view postscript files, then the most introductory article I wrote is called Echoes of Gravity, and although a few years old it may still be useful. And for a more recent discussion of measurements of the curvature of space you could look at another article I wrote, Still Flat After All These Years!.
I would like to ask an
explanation about CMBR peak. The first Doppler peak as approximately 200
divided by the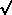 
&omega .
Actually where it comes from?
Is there any effects of
&omega&lambda
on this peak?
Прислал hsrashid"AT"pcu.helsinki.fi 5/00
This is a question about the angular position of the peak in the CMB anisotropy power spectrum. In other words, what is the characteristic angle on the CMB sky?
The answer is that there is a characteristic length built into the
known physics of the sound waves which are important for the evolution of
small-scale CMB anisotropies. This length scale (essentially the distance
a sound wave can travel in the age of the Universe at the last scattering
epoch) doesn't depend very much on the model. But the angular scale that
it appears on the sky depends on the curvature of space. The main dependence
is on whether space is flat or not, which is determined by the total
mass-energy density parameter &omegatot.
In a Universe with flat geometry the characteristic angular scale is just
below 1 degree on the sky (or a peak at about multipole 200 in the power
spectrum). In a Universe with closed geometry the angle is
larger, and in a Universe with open geometry the angle is smaller. The
dependence is approximately proportional to
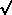&omega . The fact that the peak in
the power spectrum appears to be near multipole 200 (corresponding to an
angular scale just below a degree) is taken as very strong evidence that
the Universe has close to flat geometry. Since the total density parameter
in all forms of matter that we know of amount to perhaps
&omegamat=0.3 to 0.4, then this tells us that
some other form of energy (which does not cluster like matter) makes up the
deficit. And so there is good reason to believe that
&omega&lambda=0.6 to 0.7.
This is either a "cosmological constant" (energy density of the vacuum)
or something even stranger!
In detail the position of the peak also depends on other parameters, such as &omega&lambda, but these vairiations are quite weak. For a more detailed discussion, which is still (hopefully!) quite readable, let me refer you (again) to the article Still Flat After All These Years!, which I wrote with two of my colleagues.
ok where can i find pictures of backrounds???
Прислал Lildevil200114"AT"aol.com 5/00
The best images of the CMB sky are probably still those obtained with the COBE satellite. COBE mapped the whole sky, but with an angular resolution of about 7 degrees. So the COBE maps show a projection of the entire sky (typically into a particular oval shape that would have the plane of the Milky Way as a horizontal line through the middle) at any of 3 frequencies (or combinations of all 3), with a fairly accurate representation of the largest-scale features. They can be found at the COBE DMR images page.
The COBE maps only contain information on the biggest angular scales, since the large beam of the COBE telescope effectively smoothed the maps. But more recent experiments have mapped parts of the sky at much better angular resolution. A good example is the map from the antarctic flight of the BOOMERANG experiment, which can be found in various forms on the BOOMERANG Press Page.
I have one really big question....
I'm a student of engineering in first year so i'm not an expert in
physics or something...
Ok the question is... How CMB proves uinverse is flat?
Прислал soponcho"AT"geocities.com 5/00
I've answered similar questions above. So let me be brief here. For more details you could read, for example, the article Still Flat After All These Years!.
The basic point is that there is a characteristic scale set by the physics of the evolving density variations in the early Universe. This characteristic length scale will appear to be a different angular scale on the sky depending on the overall curvature of space (which you can think of as making parallel lines diverge or converge in open and closed spaces, respectively). Recent measurements of the CMB sky indicate that this scale is just about where you'd expect it to be in the most popular models, provided that the geometry of space is approximately flat. It could, of course, still be a bit open or a bit closed, but it has to be quite close to flat. More explicitly, the total value of the density parameter &omega = 1.0 ± 0.1 approximately.
Is "anisotropy" pronounced annieSOTTrippy or anneyeSOTTrippy ?
Прислал george.barnes"AT"tafe.nsw.edu.au 6/00
It's the latter.
We invented this word deliberately as a sort of secret hand-shake -- if you can pronounce it properly, then you're allowed into meetings of the Clandestine Members Bureau.
(Follow-up comment):
why not include a small embedded media file of the correct pronunciation of
anisotropy?
why not tell people to look
it up on Merriam-Webster's site, which includes nifty
little sound
samples to help everyone get their tongues around it. What I can't
get the hang of is not the emphasis placement, but NOT saying a long
"o" for both "o's".
Прислал frank.j.glazer"AT"verizon.com 3/03
Good idea! Although I suspect that not everyone will be able to play whatever format the file is in. Any volunteers to send me a short audio file that might be widely playable?
Now that you can pronounce it you will be allowed into the Clique for Mellifluent Badinage!
(Another Follow-up comment):
I just went to your FAQ page, looking to find out how to pronounce Anisotropy.
While I appreciate your efforts, the answer you posted was no help at all!! I
was hoping for a phonetic spelling, with syllable breaks and an accent mark!
Oh well, I'll keep looking...
P.S. Note that I do not know how to pronounce anisotropic either, so your
explanation that knowing how to pronounce this adds confusion to pronouncing
anisotropy just makes it more confusing! With explanations like this, I hope
you don't make a living teaching! Thanks for taking the time to post the FAQ
page, and please take these comments as the good hearted ribbing that it was
intended to be.
Прислал jigger"AT"Mafi-Trench.com 10/04
Ah, thanks for those words of praise! As you say, it is indeed lucky that I don't try to make a living from teaching!
As to providing a phonetic pronunciation guide, complete with upside-down letters and obscure alien accents, I'm afraid I don't know how to produce them in a way which is readable on different sorts of computers and browsers and which is comprehensible to the average cosmologist who didn't take a linguistics course!
I have a book beside my desk called a "dictionary", which specialises in this sort of thing, and indeed has a pronunciation entry for both "anisotropy" and "anisotropic". If you really want a phonetic transcription, you might try there.
But I made an attempt at copying this - here's the jpeg, and pdf versions.
Your explanation of the correspondence between CMB hotspots and last
scattering surface overdensities was intriguing. Is the overdensity the
cause of positive delta T but gravitational redshift ? Can these two cancel
out?
Прислал george.barnes"AT"tafe.nsw.edu.au 6/00
This may get a little technical, so let me take a deep breath and give this a go!
The gravitational redshift results in a decrease in the temperature for a postive enhancement in the density. The effect of the density, on the other hand, depends on what type of fluctuation we have. In the most popular sort (called "adiabatic", where the source that made these perturbations didn't change the entropy, and is what you most easily get out of inflationary models, as well as appearing to fit the current data pretty well), the density effect gives more temperature where you have more matter. So the two effects partly cancel. On the other hand there's a different kind of perturbation you can set up in the early Universe (called "isocurvature", where the overall energy density is unperturbed), in which the radiation is overdense when the density enhancement is negative. In this case (which is much less popular, since it doesn't fit the data at all well) the two effects have the same (negative) sign.
Either way, you tend to have a negative temperature fluctuation when the overdensity is positive. In principle the two effects could exactly cancel out, but that would require that the kinds of matter and energy which dominate the Universe would have to be very different from how we think the Universe behaved at the time the CMB photons last scattered and got these temperature variations imprinted.
Why is it exactly that we study the polarization of the Anisotropy? What
is it that we intend to learn from this?
Прислал noam"AT"asiaa.sinica.edu.tw 7/00
This is a very good question.
There are several parts to the answer. Firstly, the CMB is predicted to be slightly polarized through the scattering process by which it last interacted with matter. No one doubts that the polarization is there, and so it's detection will be a confirmation of the basic paradigm for the physics of the generation of CMB anisotropies. And if there is no polarization, that would be much more exciting of course!
Once the polarized CMB sky begins to be mapped in detail, then there is information which can be extracted from these signals which complements what can be determined from the temperature anisotropies. In particular the polarization is a much cleaner "snapshot" of the "last scattering surface", and so encodes more direct information about conditions back a few hundred thousand years after the Big Bang. And also the existence of very large scale gravity waves (which might be left over from certain kins of processes which happened in the very early Universe) leaves a distinct imprint on the CMB polarization. If this imprint could be detected then we would learn important information about the origin of the seed perturbations which gave rise to all the structure in the Universe.
The CMB sky is predicted to be polarized at about the level of one part in a million, so it will be challenging to map the polarization in detail. But the pay-off is sufficiently exciting that several experiments are underway to do just that.
I'm interested in knowing what the actual measurement differences were in
obtainin the background radiation values.
Прислал KBeran2140"AT"aol.com 9/00
I assume what is meant here is the size of the temperature differences measured in CMB maps. All CMB anisotropy measurements are essentially differential, i.e. experiments measure the difference between two temperatures. Since differences are measured then what is being studied are the variations in temperature relative to the average value of about 2.725 Kelvin. These variations need to be measured with an accuracy of about 10µK (or at least the average of a whole bunch of measurements of the same thing has to be this small) before you have much of a hope of detecting the anisotropies. The hottest feature seen in a CMB map has a temperature of about 100µK or 0.0001 Kelvin. And the coldest feature has a temperature of about -100µK (relative to the background temperature).
Where can I find out more about cosmic variance, sample variance
and window functions? Can you point me to any helpful papers?
Прислал TelfordRE"AT"Cardiff.ac.uk 10/00
A technical question!
For readers of this page who are wondering what the question means, let me first explain the terminology. "Cosmic variance" refers to the idea that when we measure properties of the CMB sky we might be able to do so with arbitrary precision, but the information we can extract about the properties of the cosmological model cannot be obtained with arbitrary accuracy. The reason is that our particular sky is one realisation of a statistical process described by the model (the model predicts the variance of the temperatures as a function of angular scale, not tha actual pattern of temperatures).
The fact that individual experiments only have a finite amount of information about the sky is usually referred to as "sample variance". This is just the same thing as asking any statistical question with limited information. For example asking what fraction of the time a coin comes up heads when you have only tossed it a finite number of times - this will always result in a particular level of uncertainty which depends on the number of coin tosses. For the CMB, the "sample variance" is smallest when an experiment has mapped the whole sky, and then the "sample variance" is the "cosmic variance". And you can't do better than this, because there's only one sky to observe!
A "window function" is the name given to the function which tells you the range of angular scales that a particular experiment is sensitive to. This depends on the amount of sky covered, the beam-size (angular resolution) of the telescope, and the particular scanning strategy adopted.
I'm not aware of anything terribly informative on these topics which is not written at a technical level. For details on "sample variance", you could start with a paper by myself and a couple of my collaborators (Scott, Srednicki & White, 1994, Astrophysical Journal, volume 421, pages L5-L8), which you can get here. A good paper on window functions is this one by White & Srednicki (1995, Astrophysical Journal, volume 443, pages 6-10), which you can get here, and another, by Knox (1999, Physical Review, D60, 103516), is here.
I would like to know what the fluctuations in the CMB tell us.
Прислал hurstds"AT"muohio.edu 11/00
Many, many things!
At a basic level, the fluctuations tell us that the density variations on large scales in the early Universe were about 1 part in 100,000. This turns out to be about the right amplitude for gravitational instability (i.e. the fact that overdense regions become more and more overdense with time) to have formed all the structure that we observe today over the history of the Universe. So the simple observation of these fluctuations confirms that gravity was the force that grew all of the structures (galaxies, clusters of galaxies, etc.).
By measuring how the fluctuations vary with angle, we hope to be able to determine a large number of the fundamental parameters which define precisely what sort of universe we live in. Already it appears that the CMB fluctuations tell us that the curvature of the Universe is very close to flat. And additionally that the sorts of very early density variations which the Universe possessed appear to be like those obtained in so-called inflationary models of the early Universe. We fully expect to learn vastly more in the coming years!
Could you point me to some resources that may contain
information on the calculus behind CMB.
Прислал pufffy13"AT"yahoo.com 12/00
The mathematics behind the general concepts involving the CMB is in fact quite straightforward. It's when you come to try to understand the anisotropies in the CMB that things get more challenging! I suggest that you start by going to your local bookstore or library and looking for any books they have on cosmology which are at some intermediate level between the popular text and the full-blown research textbook. Only you will be able to tell if it's the right next level for you!
Eventually you might be able to work up to the full mathematical treatment of the anisotropies. One of the most elegant and complete discourses is a paper entitled "A Complete Treatment of CMB Anisotropies in a FRW Universe" by Hu, Seljak, White and Zaldarriaga, which you can get as a postscript file here.
On the right side scale of to-day's picture there are negative
temperatures in microkelvin. I thought that, by definition, the minimum
temperature in kelvins was 0. What is your definition of the kelvin
temperature scale?
Прислал lermanma"AT"csolve.net 12/00
The picture you are referring to is a map of part of the CMB sky made by the MAXIMA experiment, which was featured on the Astronomy Picture of the Day site for 30th December 2000.
The temperature scale for that map is for temperature anisotropies rather than absolute temperatures. In other words what is measured is the temperature difference relative to the average temperature of the CMB sky. The CMB temperature is a little less than 3 Kelvin, while the temperature differences shown on the map range between about -0.0003 Kelvin and +0.0003 Kelvin (or 300µK, i.e. 10,000 times smaller). In fact the experiment only measures temperature differences, and isn't sensitive to the overall average value (which requires a different sort of experiment to measure). It would be possible to add back in the roughly 3 Kelvin "DC level" for the map, but then the anisotropies would be such low contrast that you wouldn't be able to see them.
The 2.7K CMB seems to consist of standing waves to me.
I would greatly appreciate your comment on this aspect of the
2.7K CMB. [сокращено]
Прислал henry"AT"govital.net 1/01
Let me first define a "standing wave", for others who may read this answer. Think of a standing wave as a pattern (on a string, say) with a fixed wavelength but with amplitude getting bigger and then smaller with time. There are points on the pattern (the nodes) which don't move at all), while between the nodes the displacement is biggest. There it goes through maximum, back to zero, then negative, back to zero etc. There's a nice animation here. This is what waves on the strings of a musical instrument behave like. The wave pattern itself doesn't travel along the string, and this distinguishes standing waves from "travelling waves". In travelling waves the pattern of the wave moves along at some particular speed (like waves on the surface of water for example).
The CMB does not consist of standing waves, but of travelling electromagentic waves, i.e. photons. These waves move at the speed of light, and were emitted in all directions by every part of the very early Universe.
However, standing waves do play a role in the physics of the CMB. The bumps and wiggles in the power spectrum of CMB anisotropies can be thought of as standing sound waves. By precisely measuring the anisotropies over a wide range of scales we can determine the amplitudes of all these sound wave harmonics, which tells us about the fluctuations in the early Universe, and how they evolved. This in turn tells us about fundamental properties of the Universe that we live in.
In the maps of CMB can you see two different size blobs corresponding to
the first and seconds peaks of the power spectra?
How do they make the power spectra from the map?
birdjo"AT"Spole.gov 3/01
If you stare hard at a good CMB map (or a simulated one!), you can tell that there's a characteristic angular scale. This corresponds to the scale represented by the main peak in the power spectrum. Probably it's hard to tell by eye that there's a second peak, since there's power over a wide range of angular scales. But for a sufficiently low noise map you should be able to discern that there's a characteristic size for the blobs and that there's structure on smaller scales too. For an experiment with a small enough beam-size, you would notice a lack of structure in the maps on the smallest scales, but still large enough that they're not just smoothed out by the beam - this would be the fact that the power spectrum itself has no power at the smallest scales.
Now to answer your second, more technical question, which is a good one. The crudest way to make power spectra is just to Fourier transform the map. You can bet that that's about the first thing that's done once the maps have been produced! But you need to be much more careful when producing a final estimate of the power spectrum. For a start you need to use spherical harmonics rather than Fourier modes, since the sky is curved, not flat. Then the finite size of the map introduces correlations between the modes. So you need to make binned estimates over various ranges of k, and estimate each of these in a way which is independent of the other values. A fair amount of theoretical work has been done figuring out how to do this efficiently while not losing any information content. The final estimates of power spectra from experiments like BOOMERANG and Maxima take days to run on a supercomputer!
I need to find some good colour images of the CMB for us to use as the
basis for an animation. There are 3 main images I'm after - to show the
differences between open, flat & closed Universe (ie. small, medium &
large 'blotches' of colour).
www.pioneertv.com 6/01
As a start you could look at a picture I made (with Martin White) for the US Decadal Survey in Astronomy, which you can find as a postscript file here. Basically you want a picture of coloured blobs, with stronger contrasts at smaller scales for the open model and the opposite for closed models. So in fact if you're just trying to show artistically what happens, you want to do something which looks like blowing up the small-scale features while keeping the large-scale features the same.
There's also a picture on the Boomerang web-site which is very nice for showing the connection between the CMB and the geometry of the Universe. Unfortunately it doesn't keep the same "phases" for the 3 maps, i.e. each one is a separate random simulation. So it doesn't show the effect as well as it could. But I think you get the idea that open Universes would have much more small-scale features than closed models.
what are some irregularities and what techniques are being used to
detect irregularities in CBR?
Прислал mo_poon"AT"yahoo.co.uk 10/01
The "irregularities" in the CMB are technically referred to as "anisotropies". They are deviations from smoothness discernible when a map of the microwave sky is made. These deviations occur over a wide range of angular scales. So whether you make a map of a large fraction of the sky with big pixels, or a map of a small chunk of sky with smaller pixels, you will still see variations in brightness. In fact the way that these anisotropies vary with angular scale carries the precious information about our Universe which researchers are now trying to unravel.
To make such measurements you need to be sensitive to brightness differences corresponding to only a few microKelvin, or about 100,000th of the brightness of the CMB as a whole (which corresponds to about 2.7 Kelvin). This can only be done with specially designed experiments to make ultra-sensitive maps of parts of the sky at microwave frequencies. Right now there are a range of such experiments, operating from the roofs of Physics departments, from high mountain observatories, from balloon-borne platforms or from space. Together they promise to build up the full picture of the cosmological information content buried in the CMB sky.
What are the implications for various cosmological models of the
universe?
Прислал mo_poon"AT"yahoo.co.uk 10/01
Things are really the other way round: we learn about the cosmological model by measuring the anisotropies. The precise variation of the anisotropies with angular scale (how "noisy" the maps look as a function of the size of the pixels) encodes information about the Universe in which we live. We can learn about the initial seeds from which all the structure formed, as well as the amount and composition of dark matter, the rate of expansion, the flatness of space, the overall shape of the Universe etc. That we have the ability to learn all these things by measuring the microwave sky is an incredible opportunity that the Universe has given us.
Since the CMB was emitted prior to star and galactic
formation, why do we not see images in "negative" of
these material structures? I.e., surely the moon
blocks the CMB from a telescope. Surely the sun does
as well. Why not Alpha Centauri? Andromeda?
Прислал bopbone"AT"yahoo.com 11/01
Absolutely!
The Sun is a local strong emitter of radiation at just about every wavelength. So to make a map of the CMB sky, you have to make sure the Sun isn't in your picture! It's even worse than that though, since you're looking for variations of one part in 100,000. So you have to make sure you don't even see a glancing reflection of the Sun. CMB experiments go to great trouble to reduce any effect of the Sun by observing well away from the Sun's position, as well as having all sorts of shields etc.
The Moon reflects all sorts of light from the Sun, and also glows in the mcrowaves (because the Sun heats it up). So you have to avoid the Moon too.
Even the most nearby stars are still so far away that their effects are negligible. However, that's not true for the whole agglomeration of stars in our Galaxy (the Milky Way). So you have to make CMB maps well away from the Galactc Plane.
Other galaxies will have a smaller effect. This certainly has to be thought about. They block the CMB, it's true, but they also emit radiation on their own. So they will typically be bright spots. There's another effect though that can casuse a "hole" in the CMB at certain wavelengths. That's called the "Sunyaev-Zel'dovich" effect (after the two Soviet scientists who first suggested it might be observable). The idea is that hot gas in the outskirts of galaxies, or in clusters of galaxies can scatter some of the CMB photons. Some of the low energy photons gain energy, and so with a radio telescope you see a hole in the CMB in the direction of a galaxy cluster (and at shorter wavelengths you'd see a hot spot in the same place). This effect has in fact been observed for many of the biggest clusters of galaxies. And presumably as observatioins continue to get better, we'll eventually be able to see this effect for individual galaxies too. It actually turns out to be a useful thing to observe, since it tells you information about the obstructing object that would be hard to tell any other way.
In the CMB rest frame you measure no velocity with respect to the CMB
photons?
I thought that the speed of photons was "c" when measured from any and
all frames of reference. What am I missing?
Прислал 12/01
It may be that some people (even me, gasp!) have been sloppy with language when explaining the CMB "dipole" effect.
Of course the photons are always moving at the speed of light. So what you detect is not that there's a different speed for the photons in one direction. You simply see more photons (or equivalently a brighter intensity or higher temperature) in the direction you're moving towards, and fewer in the opposite direction. Think of it as a bunch of photons moving about in all directions, and then imagine how many photons will cross a unit area of detector per unit time. If you are in the rest frame with respect to the CMB photons, then you measure the same flux of photons no matter where you point your detector. But if you now move your detector very fast in one direction then you'll get more photons per unit time. It's just like how you get more raindrops in your face when you run in a rainstorm!
So the effect is that if we're moving in some direction relative to the "CMB rest frame", then there will be more photons (per unit area per unit time) apparently coming from that direction, and fewer coming from the opposite side of the sky. That the sense in which we can detect whether we're moving with respect to the CMB photons.
I was recently reading how the COBE has observed very slight variations in
intensity of microwave radiation as a function of direction, but I do not know
what causes this. Could you provide any insight as to the source of these
variations?
Прислал gte878n"AT"prism.gatech.edu 3/02
Since you can find more detailed answers here on this very web-page, let me just provide you with a brief answer here. They are variations in density observed at the epoch when the photons last interacted with the matter in the Universe, about half a million years after the Big Bang, when the Universe was very much hotter and denser. Sveral other experiments have detected such variations, at a range of angular resolutions, and we're now building up a detailed picture of these minute variations in temperature, which hold valuable information about the structure of the Universe on large scales.
I'd like to know if it would be possible to orient oneself in space by
comparing extremely accurate CMB maps. For example, if one was to make a
hi-res CMB survey map and if one could (by magic!) travel to another part
of the universe hundre ds of millions light years away *instantly*, would
it be possible to determine o ne's location (relative to the origin point)
by taking new CMB measurements and comparing them to the original
measurements? If not, how might such a feat be accomplished?
Прислал damiensk"AT"pacific.net.au 8/02
This is a very interesting question!
The CMB anisotropies come from the "last scattering surface", which is an imaginary sphere around us, where we can see back to a time when the radiation last interacted with matter. The hot spots and cold spots on the sky come from the overdensities and underdensities on this sphere. Each observer has a different surface, determined simply by the distance that light can have travelled in each direction in about the last 15 billion years. So if we moved, say 1000 light years in some direction, then the CMB map would look pretty much identical. But if we moved some significant fraction of 15 billion light years, then we'd be seeing different density blobs, which would cause different sets of hot spots and cold spots. In fact the "thickness" of the last scattering surface is something like a few hundred thousand light years, and so if you moved further than that, then the features you'd see on the CMB sky would no longer be correlated.
So I suppose if you found yourself instantly in a part of the Universe where the CMB sky looked similar, but a little different from our own, then you could infer that you'd moved by some amount in some direction. It should be possible to quantify that amount, and know where you were. However, if you moved to some part of the Universe millions of light years away, then the maps would have nothing in common (other than the overall level of fluctuations etc.), and so you'd have no idea where you were, other than further than something like a million light years.
How do the COBE results conform with a model with a positive cosmological
constant? Is this model scale invariant too? If not, why do the
physicists bother themselves about it? [сокращено]
Прислал 11/02
The results of the COBE satellite indicated that the initial conditions for the density perturbations (which were laid down in the early Universe and which gave rise to all of today's structure) were "scale invariant". This means equal amounts of fluctuations at all scales. This says nothing about the geometry of the Universe, or about whether or not there is a cosmological constant.
The COBE data are equally well fit with the sort of model which is currently popular, i.e. about 2/3 of the total energy density in a cosmological constant (or "Dark Energy") and the other 1/3 in Dark Matter. However, it's also true that very large amounts of Dark Energy would have left a noticeable effect on the COBE data, which were not seen (so we know the Universe isn't very closed, with more than enough cosmological constant, for example).
In fact the most recent CMB anisotropy data, from several experiments which collected data at smaller angular scales than COBE, also point towards models which contain about 2/3 Dark Energy.
My question concerns
the image generated in the early 90's from the COBE satellite. What was the
significance of this image, apart from confirming the existance of the CMB?
Did the image change our ideas of the background radiation in any way?
Прислал Andres.Donaldson"AT"stpauls.richmond.sch.uk 11/02
The data from the COBE DMR instrument were the first to demonstrate that the CMB sky contained anisotropies. So the fluctuating pattern in the images showed regions of the early Universe which were a little hotter or cooler than average. The CMB itself had been detected in 1965, but all images made of the CMB had shown it to be extraordinarily smooth (apart from the "dipole' pattern showing our motion through space).
The COBE data measured the amplitude of these temperature variations. And they were pretty much exactly what was needed for the popular "cold dark matter" models to have left those impressions in the early Universe and then grown all of today's structures through gravitational instability by the present day.
So the anisotropies in the COBE data were very important in confirming that the basic cosmological picture was on the right track. That picture is composed of: a hot early Universe, expanding and cooling, containing low contrast density perturbations at early times, which grew over billions of years to produce all of the rich structure of today's Universe. If COBE had detected no anisotropies, or ones with the wrong amplitude or variation with angular scale, then our basic paradigm would have to have been dramatically changed (and there were many cosmologists at the time who were anticipating such a change!).
Newer CMB anisotropy results have further bolstered this picture, as well as filling in some of the details, like the form of the initial density perturbations, the amounts of dark matter and dark energy, etc.
I've read some introductory notes on CMB anisotropy. I saw that most
calculations assume the matter content of the universe as it is, without
considering the fact that the matter content must somehow evolve via
CP-violation processes to produce a net amount of matter.
I wonder if there has been any attempts before to include this
CP-violation processes in CMB anisotropy calculation and if there will be
any observables due to this.
Прислал haryo"AT"hep.fsu.edu 01/03
It's clear that the vast majority of the Universe is made of matter rather than "anti-matter", and that there has to be a good particle physics explanation for this eventually. At the moment there is no definitive answer to the process which favoured matter over anti-matter, although there are a number of ideas.
The effects which generate this asymmetry occur at very high energies, long before the CMB anisotropies that we see were generated. I'm not aware of any detectable effects of such processes on the CMB anisotropies. But I'd be happy to hear of the details of any idea that you work out!
The uniformity of CBR suggests that the Universe was
very smooth during the first 300000 years. On the
other hand dark matter should have been in clumps that
attracted ordinary matter after the decoupling of
radiation and matter, to form galaxies. But these
clumps of dark matter would affect the geomerty of the
Universe. So the Freedman's smooth viewpoint of the
primeval Universe is wrong and should be replaced by
inhomogeneous models.In this case the CBR ought to
have irregularities. What's wrong with this picture?
Прислал tomp044"AT"yahoo.co.uk 02/03
This is a very good question!
The answer is something that cosmologists refer to as "gravitational instability". This is the fact that slightly overdense regions increase their contrast relative to the average density (and obviously undersense regions get more underdense) as the Universe gets older. This happens in a regular static medium, and turns out also to happen in an expanding medium (i.e. the Universe as we know it), although at a slower rate. You can think of an overdense region expanding a little slower than a typical part of the Universe and hence increasing its density contrast with time.
The Universe at early times had very low amplitude inhomogeneities. We see these at a time of about 300,000 years through the CMB anisotropies, which have amplitudes of about 1 part in 100,000. These amplitudes have grown by the present time (say 14 billion years later) to form galaxies and the rest of the structure in today's Universe.
What is anisotropy?
Прислал mriccobo"AT"ucsd.edu 03/03
The dictionary definition is something like "the state of having different properties in different directions". In CMB studies (as in some other fields, like geophysics, crystallography, etc.) this word is used to refer to the quantification of the degree to which something is not isotropic. Specifically, CMB anisotropies are the description of the temperature variations on the microwave sky, i.e. the pattern of hot and cold spots which we can detect using sensitive CMB experiments.
I'm doing my ninth grade science fair project on the theory of a finite, dod
ecahedral universe. ... Most of the words I don't know the meaning of I can do
without, but the main one that I can't seem to get around is "spectrum".
Do you think you
could explain to me the meaning of this word, and what exactly its relationship
to my topic would be?
Прислал jewelz1088"AT"comcast.net 01/04
Here "spectrum" has a slightly more general meaning than you might have come across. A spectrum is usually the light spread out into all its wavelengths (colours). This might be more properly called the frequency spectrum.
But we can also imagine taking an image and splitting it up into the amplitude of waves in space - we can plot amplitude versus (spatial) wavelength, for example, as a way of describing the information in the image. More usually physicists like to plot the amplitude squared against the inverse of the wavelength, and that's called the "power spectrum". A plot of this power spectrum is a good way of statistically describing the content of an image. In particular it gives a way of seeing how much "power" the image has at different scales (i.e. is it very blotchy on small scales, or large scales, or what?). This is the standard technique for describing the statistical content of CMB maps. For large enough maps (where the sky isn't flat, but curved) you need to use something slightly different, which works on the surface of a sphere rather than on a flat plane, but it's still called the power spectrum.
The point is that theoretical models of the Universe can predict the shape of this power spectrum. And so by careful statistical comparison of the observed power spectrum with a set of theoretical ones, we can infer things about the model which describes our Universe.
Would you be kind enough to tell me who was the first cosmologist to propose
acoustic oscillations (as opposed to density fluctuations)as the origin of the
CMB anisotropies. The more I think about it, and the more I'm convinced it is
one of the most brilliant ideas in the whole field of modern cosmology!
Прислал georges_melki"AT"hotmail.com 02/04
This is an excellent question!
The main idea is that density perturbations oscillate as sound waves, driven by gravity and with the restoring force provided by pressure between the baryons (regular matter) and photons. The CMB sky can be thought of as a snapshot of these oscillating modes - kind of like a set of standing waves with random phases, spread over the sky. The evolution of the sound waves makes particular angular scales special, resulting in the peaks and troughs seen in the power spectrum of CMB anisotropies.
The best answer is that the idea was already fairly clearly formulated by Jim Peebles and Yacob Zel'dovich (and their collaborators) around 1970. There are papers by these US and Soviet groups about that time which show power spectra with such oscillations present. At that time there was most focus on the signature of the oscillations on the matter disctribution (non-baryonic dark matter wasn't really talked about then!), but over the next few years there were published predictions of CMB anisotropy power spectra too. Particularly important papers with such predictions were those by Doroshkevich, Zeldovich & Sunyaev in 1978 and Silk & Wilson in 1981. Precisely which paper contained the definitively earliest prediction of the CMB acoustic peaks is probably a matter which will be debated by future historians of science!
The idea for acoustic oscillations at all in the Universe goes back to Andrei Sakharov (also famous as a dissident) in the mid-1960s. However, Sakharov's picture was of a cold universe, since this was before the CMB had been discovered. Hence there were no anistropy oscillations in his picture, since there was no CMB at all!
Some people like to give some of the credit to Sakharov. But my own view is that although he played an important role, the real progress was made by Peebles, Zel'dovich and co., when they formulated the modern ideas around 1970.
Could you pls elaborate on the Fourier development of the CMB power spectrum in
your FAQ section.To my knowledge,Fourier analysis applies to periodic functions,
and I can't see anything periodic in the CMB!
Прислал georges_melki"AT"hotmail.com 02/04
You can certainly carry out Fourier analysis for functions which are not periodic, provided that they're bounded. For example, if you have an image of something in a rectangular array of pixels, then you can Fourier transform the image to understand the amplitudes of all the waves (which fit to have nodes at the boundaries of the image) that you have to add together to contruct the image. In 2-dimensions you can separate the problem into waves in the x-direction and waves in the y-direction. If there's no special direction in the image, then the information in the 2 directions will be statistically the same, and you'll care about the amplitudes (and possibly phases) of the modes as a function of the modulus of the vectors in Fourier space.
The analysis of CMB images is exactly the same, at least for small maps. There are no special directions in the CMB sky, and the phases of the CMB anisotropies are random (this is both justified from theoretical prejudice and from empirical testing of real CMB data). So you can statistically describe the structures in the map by looking at the power spectrum of Fourier modes, i.e. estimates of the squared amplitudes of the Fourier modes as a function of scale (or technically the wavenumber, the reciprocal of scale).
For CMB maps which are larger, you can't ignore the curvature of the sky. So you can't use Fourier analysis, which only work for a flat image. Instead you use a different set of functions to decompose the CMB sky - functions which are appropriate to use on a sphere. These are called spherical harmonics. The CMB power spectrum is plotted as a function of "multipole", which is an inverse angle. This is simply the curved sky version of the Fourier power spectrum of a flat 2-D image.
was universe really re-ionized ? how to detect it's
signatures on the CMBR. What is means by optical
depth and how to measure it for reionization ?
Прислал jprasadb"AT"yahoo.co.in 04/04
The Universe became neutral at about 300,000 years after the Big Bang, which is the time the CMB photons last scattered. Except that the Universe became ionized again fairly recently (by cosmic standards) at maybe a few hundred million years after the Big Bang - and this has a small effect on the CMB photons. "Optical depth" is the term used to quantify the amount of scattering. The bigger the optical depth between us and the epoch of reionization, the bigger the effect on the CMB. These effects are measurable on the CMB anisotropies, and give a particularl signal in the large-angular scale CMB polarization data. Such a signal was seen by the WMAP satellite, and through measuring it in more detail we should be able to learn about the processes which reionized the Universe.
so, if the big bang was lumpy, we could see changes in the CMB flux
as time goes on, or if we could go to another point in the universe?
Прислал rich"AT"concordma.com 07/04
This applies to the lumpiness of the Universe at the "last scattering surface", when the CMB photons last interacted with matter. We see a certain pattern of anisotropies on the CMB sky because of these irregularities. If we could instantaneously move to a different part of the Universe, then we'd be seeing a spatially different surface in the past, and hence see a different pattern of anisotropies. However, you'd have to travel a cosmologically significant distance in order to see much difference! And the amplitudes of the temperature variations as a function of angular scale on the sky (a.k.a. the anisotropy "power spectrum") would be statistically the same as we see on our sky.
It's also true that if we wait long enough we'll be able to see the CMB sky changing, as the last scattering surface moves back through space. But again, you'd have to wait a cosmologically significant amount of time before you'd notice the difference!
I have read some papers,books,reviews.But I can't understand why in angular
power spectrum of CMB the main contribution in low multipoles(l) is mainly due
to SW-ISW effect?I mean t o say that we can explain low "l" contribution to
angular power spectrum conside ring SW-ISW effect,why?
Прислал kanan"AT"cts.iitkgp.ernet.in 04/05
This is alittle hard for me to answer, since I don't know how much you already understand. But let me have a stab anyway.
"SW" is the Sachs-Wolfe effect, first pointed out in a paper by Sachs and Art Wolfe in 1967. The physical effect is that fluctuations in gravitational potential cause fluctuations in CMB temperature. Basically we can see correlated variations in gravitational potential on the last-scattering surface on a wide range of angular scales. These scales include those which are large enough that causal physical processes cannot have affected them between the time the fluctuations were laid down (the inflationary epoch, say) and the last-scattering time. This corresponds to an angular scale of about a couple of degrees on our sky. So on angular scales measured in degrees we're seeing the "initial conditions" in the variations in gravitational potential, unaffected by causal processes - in other words we see the Sachs-Wolfe effect at low multipoles.
I hope this helps!
At http://snews.bnl.gov/popsci/spectroscope.html it is said that "a
Doppler-shifted blackbody spectrum from a body at one temperature doesn't
look exactly like a blackbody spectrum produced at any other temperature".
Is that statement really correct and does it mean that the Doppler shifted
CMB dipole is not a blackbody?
Прислал vorleons"AT"hotmail.com 08/05
The CMB dipole does not have a blackbody spectrum, but a spectrum which is the frequency derivative of a blackbody. You can see this by realising that the dipole is the CMB pattern minus the "monopole", i.e. you need to take a difference. For any anisotropy measurement, the function you use to convert from intensity fluctuation to temperature difference is the derivative of the Planck (blackbody) function.
And actually it's a little more complicated that that, since really all we've done by using the derivative of the Planck function is use the first term in the Taylor expansion. In principle higher order corrections are also there, and potentially measurable as small (calculable) deviations from the monopole (times the Planck function) plus the dipole (times the derivative of the Planck function).
If one could actually measure the absolute spectrum at every point (rather than making relative measurements), then of course it would be an exact blackbody everywhere, with the temperature varying with position.
If you'd like more technical details, there's a paper in 2003 by Kamionkowski and Knox, called "Aspects of the Cosmic Microwave Background Dipole", which you can find here
Could you also comment on the accuracy of the following comment in a
Wikipedia article about the CMB (http://en.wikipedia.org/wiki/CMB): "There
are however very small yet significant variations (anisotropies) from the
black body spectrum. The most pronounced is the dipole anisotropy (180
degree scales) which is at a level of about 10^−3 of the monopole." I
thought that no spectral deviation from a blackbody has so far been detected
in the CMB and that those anisotropies are just temperature variations from
point to point.
Прислал vorleons"AT"hotmail.com 08/05
I wonder who wrote that?!
I think it should say something like "There are however very small yet significant variations (anisotropies) from the uniform temperature observed on the sky".
Maybe you'd like to edit the wikipedia entry? You're obviously smarter (or at least more careful) than whoever is responsible for that statement!
[сокращено] ... whereas they go into elaborate mathematical developments, there
is always something arbitrary on the physics side(or so it seems to
me at least).Take for example Zaldarriaga's "An Introduction to CMB
anisotropies", which I find excellent regardless of the numerous
typos.Here is a typical statement from this paper:
"We start by considering perturbations produced by density
modes.When working with linear theory in a flat universe, it is
convenient to use Fourier modes because they evolve
independently.These modes are the eigenfunctions of the Laplacian
operator.."
Well, apart from the last statement, which is trivial[exp(ik.x) is
definitely an eigenfunction of the Laplacian...], all the rest
seems to me to be imposed on the reader! To start with, I don't
agree with the "flat universe" bit,it is misleading:the universe
may be spatially flat...
Then,why is it convenient to use Fourier modes to describe density
perturbations?Because they evolve independently? And how do we know
they are the only modes?Is this a postulate?
A few pages further, we have another "deus ex machina"
statement:"The anisotropy field is characterized by a 2x2
tensor".Again, what is the reason for this?
Прислал brans_dicke"AT"yahoo.com 09/05
All of those statements seem pretty obvious to me, but then I was trained as a physicist and not a mathematician!
When we say the Universe is "flat", we mean that its spatial sections are Euclidean. That's a very good approximation in the early Universe, since it's pretty much true today and all the models evolve away from flatness.
The Fourier modes are a complete set of modes. In other words I can write down any scalar function of position (describing the density field) and construct it as a superposition of 3D Fourier modes.
It's convenient to use Fourier modes, because they evolve indpendently in "linear perturbation theory". Linear theory is a very good approximation at early times since the dimensionless amplitude of the perturbations is about 10-5.
And the business of the 2x2 tensor, that's for describing the full polarized CMB anisotropy field. The reason for this choice is just geometry - that's the mathematical object you need to describe the algebra of linear polarization. You can look this up in standard textbooks on polarization - there's nothing about this which is specific to the CMB.
I hope this helps to dispell at least some of the apparent acts of faith!
In a nut-shell, CMB anisotropies can be thought of as the line-of-sight
projection of various plane-wave temperature and polarization
fluctuations.
Amazingly, the acoustic peaks are due to contributions in a direction of
observation which is orthogonal to the wave-vector.
Isn't there a paradox here? And how do you explain this?
Прислал georges_melki"AT"yahoo.com 10/05
You're right. Except that the "spatial" part of the phases of the plane-waves is completely random (to a high degree of accuracy at least). So you can think of a sea of fluctuating lumps, whose specific positions aren't organised in any way (or alternatively think of a set of plane waves with all sorts of directions and random positional phases). It's the "temporal" phases of all the fluctuations which are coherent, i.e. all the lumps of a particular scale are oscillating in and out together, like balloons being inflated and deflated (or like a set of standing waves if you're thinking in the wave picture).
The CMB "last scattering surface" is just like a slice through the 3-dimenstional distribution of lumps at a particular time. There are places (in space, or projected on the sky) where the amplitude is high (both positive and negative) and places where it's low. But on a particular scale they're all evolving together in time. So the variance of the amplitudes of the fluctuations is just a function of time, for a given scale. Now if we take a snap-shot of the pattern, we see this variance being a function of scale, which we measure as the angular spectrum of the CMB anisotropies. And it doesn't really matter whether you think of this scale as being in the line-of-sight direction or the transverse direction, because there are no special directions in the Universe.
could you please explain why the fluctuations in CMB map produced by the
WMAP satellite allow cosmologists to observe structure in the universe further
back in time than do observations of galaxies at high red shifts.
Прислал Lilac4moi"AT"aol.com 10/05
When we see the CMB, we are seeing the structures in the Universe at the time the photons were last scattered. This turns out to be about 300,000 years after the Big Bang. The CMB photons have been stretched by a factor of about 1000 since that time, i.e. we're observing back to redshifts of about a thousand. So by measuring the CMB anisotropies we can learn about the structure in the Universe at very early times, when the density contrasts were still low (i.e. before any actual objects had formed).
When we observe galaxies, we're seeing the photons that were made in stars in those galaxies. The most distant galaxies are seen at redshifts of about 6 - and obviously most galaxies we see are at much lower redshifts than that. So we know a lot about structure in the Universe are relatively low redshift. Obviously you can't see galaxies unless there's starlight, and we think the first stars were formed at redshifts below 20 (although this value is still very poorly known). Se we're never going to see individual galaxies back to redshifts anywhere like as high as where we're seeing the CMB anisotropies.
The neat thing is that by comparing the structure at low redshift with the structure at earlier times seen on the CMB sky, we can learn a huge amount about how structure has formed in the Universe.
In an article by Hu and White entitled "A CMB polarization primer", one
reads the following statement:"The degree of linear polarization is
directly proportional to the quadrupole anisotropy in the photons when
they last scatter".
So, is this the same quadrupole that gives the differential background
temperature between two points on the sky separated by 90 degrees?Or is
it some property of the radiation at every
point in the sky?
Прислал georges_melk"AT"yahoo.com 10/05
It's both of what you suggested.
Every observer in the Universe sees their own last-scattering surface. You can also think of the scatterers on our surface seeing their own "sky". On that sky there will be a quadrupole, and this is what acts as the "source" for the polarization. The polarization we observe is the sum over all the patterns made by all these scatterers.
Douglas Scott dscottATastro.ubc.ca Последняя редакция: 15 Сентября 2005
..:: Перевел с английского В.Г. Мисовец
